Please Make A Note: 9. Derivation of the Continuity Equation in Spherical Coordinates

Sunday, July 4, 2010

We start by selecting a spherical control volume dV. As shown in the figure below, this is given by

$\bg_white \120dpi {\rm d}\mathcal{V}=r^2 \sin \theta \,{\rm d}r \,{\rm d}\theta \,{\rm d}\phi$

where r, θ, and φ stand for the radius, polar, and azimuthal angles, respectively. The azimuthal angle is also referred to as the zenith or colatitude angle.

The differential mass is

$\bg_white \120dpi \text{d}\mathcal{M}=r^2 \sin \theta {\rm d}r {\rm d}\theta {\rm d}\phi$

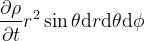
We will represent the velocity field via

$\bg_white \120dpi \mathbf{u}=u \, \mathbf{e}_r + v \, \mathbf{e}_\theta + w \, \mathbf{e}_\phi$

In an Eulerian reference frame mass conservation is represented by accumulation, net flow, and source terms in a control volume.

Accumulation

The accumulation term is given by the time rate of change of mass. We therefore have

$\bg_white \120dpi \frac{\partial \rho}{\partial t}r^2 \sin \theta {\rm d}r {\rm d}\theta {\rm d}\phi$

The net flow through the control volume can be divided into that corresponding to each direction.

Radial Flow

Starting with the radial direction, we have

$\bg_white \120dpi \dot{m}_{\rm in}=\rho \, u \, A_{\rm in}$

The inflow area A_in is a trapezoid whose area is given by

$\bg_white \120dpi A_{\rm in} = \text{mid segment}\times{\rm height}=\tfrac{1}{2}\left[r \sin \theta {\rm d}\phi + r \sin(\theta + {\rm d}\theta){\rm d}\phi \right ]\times r {\rm d}\theta$

The key term here is the sine term. Note that the mid segment is the average of the bases (parallel sides). Upon expansion of A_in, and in the limit of vanishing dθ, we have

$\bg_white \120dpi \sin(\theta + {\rm d}\theta)=\sin\theta \cos{\rm d}\theta + \cos\theta \sin {\rm d}\theta \approx \sin \theta + \cos \theta {\rm d}\theta$

substitution into A_inyields

$\bg_white \120dpi A_{\rm in} = r^2 \sin \theta {\rm d}\theta {\rm d}\phi + \tfrac{1}{2}r^2 \cos \theta {\rm d}\theta^2{\rm d}\phi \approx r^2 \sin \theta {\rm d}\theta {\rm d}\phi$

where high order terms have been dropped.

The outflow in the radial direction is

$\bg_white \120dpi \dot m_{\rm out}=\left(\rho u +\frac{\partial \rho u}{\partial r}{\rm d}r \right )A_{\rm out}$

but

$\bg_white \120dpi A_{\rm out} = \text{mid segment}\times {\rm height}$

where

$\bg_white \120dpi \text{mid segment} = \tfrac{1}{2}\left[(r + {\rm d}r)\sin\theta{\rm d}\phi + (r + {\rm d}r)\sin(\theta + {\rm d}\theta){\rm d}\phi \right ]$

and

$\bg_white \120dpi \text{height} = (r + {\rm d}r){\rm d}\theta$

By only keeping the lowest (second & third) order terms in the resulting expression, we have

$\bg_white \120dpi A_{\rm out}=r^2 \sin \theta {\rm d}\theta {\rm d}\phi + 2 r \sin \theta \, {\rm d}r \, {\rm d}\theta \,{\rm d}\phi$

Note, that in the expression for Aout, we kept both second order and third order terms. The reason for this is that this term will be multiplied by "dr" and therefore, the overall order will be three. In principle, one must carry all those terms until the final substitution is made, and only then one can compare terms and keep those with the lowest order.

At the outset, the net flow in the radial direction is given by

$\bg_white \120dpi \dot{m}_{\rm out}-\dot{m}_{\rm in}=2 \rho \,u \,r \sin \theta \, {\rm d}r \,{\rm d}\theta \,{\rm d}\phi+ \frac{\partial \rho \, u}{\partial r}r^2 \sin \theta \, {\rm d}r \,{\rm d}\theta \,{\rm d}\phi$

Polar Flow (θ)

The inflow in the polar direction is

$\bg_white \120dpi \dot{m}_{\rm in}= \rho \, v \, A_{\rm in}$

where

$\bg_white \120dpi A_{\rm in} = r \sin \theta \,{\rm d}r \,{\rm d}\phi$

The outflow in the θ direction is

$\bg_white \120dpi \dot{m}_{\rm out}=\left(\rho\, v + \frac{\partial \rho\,v}{\partial \theta}{\rm d}\theta \right )A_{\rm out}$

where

$\bg_white \120dpi A_{\rm out}=\tfrac{1}{2}\left[r \sin (\theta + {\rm d}\theta){\rm d}\phi + (r+{\rm d}r)\sin(\theta + {\rm d}\theta){\rm d}\phi \right ]{\rm d}r$

Upon expansion, and keeping both second and third order terms, we get

$\bg_white \120dpi A_{\rm out}\approx r \cos \theta \, {\rm d}r \,{\rm d}\theta \,{\rm d}\phi + r\sin\theta \, {\rm d}r \, {\rm d}\phi$

Finally, the net flow in the polar direction is

$\bg_white \120dpi \dot{m}_{\rm out} - \dot{m}_{\rm in}=\rho \,v\, r \cos\theta \,{\rm d}r \,{\rm d}\theta \,{\rm d}\phi+ \frac{\partial \rho v}{\partial \theta}r \sin \theta \,{\rm d}r \,{\rm d}\theta \,{\rm d}\phi$

Azimuthal Flow (φ)

The inflow in the azimuthal direction is given by

$\bg_white \120dpi \dot{m}_{\rm in}=\rho\,w A_{\rm in}$

with

$\bg_white \120dpi A_{\rm in} = r \,{\rm d}r \,{\rm d}\theta$

while the outflow is

$\bg_white \120dpi \dot{m}_{\rm out} = \left(\rho w + \frac{\partial \rho w}{\partial \phi}{\rm d}\phi \right )A_{\rm out}$

and

$\bg_white \120dpi A_{\rm out}= r \, {\rm d}r \, {\rm d}\theta$

At the outset, the net flow in the polar direction is

$\bg_white \120dpi \dot{m}_{\rm out}-\dot{m}_{\rm in} = \frac{\partial \rho w}{\partial \phi}r \, {\rm d}r \,{\rm d}\theta\,{\rm d}\phi$

Continuity Equation

Now, by collecting all mass fluxes we have

$\bg_white \120dpi \frac{\partial \rho}{\partial t}{\rm d}\mathcal{V}+2 \rho \,u \,\frac{{\rm d}\mathcal{V}}{r}+ \frac{\partial \rho \, u}{\partial r}{\rm d}\mathcal{V}+\rho v \cos \theta \frac{{\rm d}\mathcal{V}}{r \sin \theta} + \frac{\partial \rho v}{\partial \theta}\frac{{\rm d}\mathcal{V}}{r} + \frac{\partial \rho w}{\partial \phi}\frac{{\rm d}\mathcal{V}}{r \sin \theta}=0$

which, upon dividing by dV and combining terms, reduces to

$\bg_white \120dpi \frac{\partial \rho}{\partial t}+\frac{1}{r^2}\frac{\partial \rho \,r^2 u}{\partial r}+\frac{1}{r \sin \theta}\frac{\partial \rho v \sin\theta}{\partial \theta} +\frac{1}{r \sin \theta} \frac{\partial \rho w}{\partial \phi}=0$

which is the continuity equation in spherical coordinates.

Voila!

[Previous: Continuity Eq. in Cylindrical Coordinates]

[Table of Contents]

[Next: How Euler Derived the Momentum Equations]

Cite as:
Saad, T. "9. Derivation of the Continuity Equation in Spherical Coordinates". Weblog entry from Please Make A Note. http://pleasemakeanote.blogspot.com/2010/02/9-derivation-of-continuity-equation-in.html

11 comments:

AlexSeptember 19, 2010 at 6:27 PM
Thanks a lot for the derivation, I was having some issues picturing the spherical element.

A better way of doing it is by doing the grouping done in the last line using the product rule when you calculate each difference in mass flow rate.

Also if you leave some second order terms, when you divide by dV, then you can say and as dx_k go to 0, those terms go away.
AnonymousNovember 28, 2010 at 7:43 AM
There is an error in the last line. In polar coordinates, it should be derivative of ro*v*sin(theta) wrt theta instead of derivative of just ro*v wrt theta.
yNotNovember 28, 2010 at 4:54 PM
yes, thanks for catching that typo.
poojaJanuary 23, 2012 at 6:06 AM
pls explain it i m not able to unnderstand how did u make dis diagram amd draw its coordinate and y did u do dis
Nitrox7January 7, 2013 at 10:43 PM
What software did you use to draw the element?

Was trying to do it in Visio, but it rather complicated so I'm thinking that there must be a software already out there with this capability.

And thanks for the derivation, very nice job!

Thanks!
UnknownApril 18, 2013 at 8:21 AM
Hello,

Thanks for diligent work. I couldn't still understand the way you calculated the volume ,dV.
hasuladJune 19, 2013 at 8:05 AM
Fantastic blog and very useful information. Thank you very much !
UnknownOctober 24, 2013 at 4:35 AM
oh,it is very very useful.thank you so much.
DipakJanuary 22, 2015 at 9:35 AM
Thanks for this, having a really hard time in aerodynamics

Pages

Sunday, July 4, 2010

9. Derivation of the Continuity Equation in Spherical Coordinates

Accumulation

Radial Flow

Polar Flow (θ)

Azimuthal Flow (φ)

Continuity Equation

11 comments: