8. Derivation of the Continuity Equation in Cylindrical Coordinates

This is one of my favorite derivations. Although it would sound a bit intimidating at first, as none of the standard textbooks carry out the derivation in curvilinear coordinates; it is rather easy to obtain. And guess what? the math is quite rewarding!
So we first have to start by selecting a convenient control volume. The idea here is to pick a volume whose sides are parallel per say to the coordinates. For cylindrical coordinates, one may choose the following control volume

Again, as we did in the previous post, we need to account for all the fluid that is accumulating, and flowing through this control volume, namely:
Rate of Rate of Flow In = Accumulation  + Rate of Flow Out
or
Accumulation + Flow Out - Flow In = 0

First, let’s get some basics laid out. The velocity field will be described as

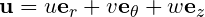
I always prefer to use u, v, and w instead of ur, utheta, and uz to save on subscripts, although the latter nomenclature is a bit more descriptive… we’ll get used to it. Now, by construction, the volume of the differential control volume is

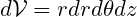
while the mass of fluid in the control volume is

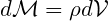
The rate of change of mass or accumulation in the control volume is then

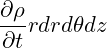
For the net flow through the control volume, we deal with it one face at a time. Starting with the r faces, the net inflow is

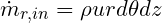
while the outflow in the r direction is

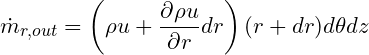
So that the net flow in the r direction is

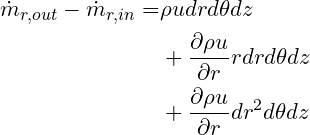
Being O(dr^2), the last term in this equation can be dropped so that the net flow on the r faces is

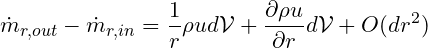
The net flow in the theta direction is slightly easier to compute since the areas of the inflow and outflow faces are the same. At the outset, the net flow in the theta direction is

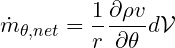
We now turn our attention to the z direction. The face area is that of a sector of angle d\theta:

then, the inflow at the lower z face is

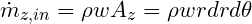
while the outflow at the upper z face is

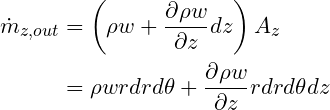
Finally, the net flow in the z direction is

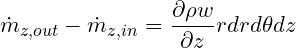
Now we can put things together to obtain the continuity equation

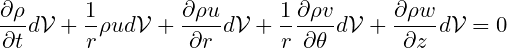
dividing by dV and rearranging the r components of the velocity

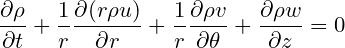
Voila!
[Previous: Continuity Eq. in Cartesian Coordinates]

[Table of Contents]

[Next: Continuity Eq. in Spherical Coordinates]

Cite as:
Saad, T. "8. Derivation of the Continuity Equation in Cylindrical Coordinates". Weblog entry from Please Make A Note. http://pleasemakeanote.blogspot.com/2009/02/8-derivation-of-continuity-equation-in.html