[PLEASE NOTE, THAT DUE TO TIME RESTRICTIONS, I WILL NOT BE ABLE TO PUBLISH THE FULL MPI WARMUP TUTORIAL IMMEDIATELY, THEREFORE, I WILL PUT THE PARTS ONE AT A TIME. SO KEEP CHECKING THIS POST. THANK YOU FOR READING THIS BLOG.]
In this article, I will go over several examples of how to use some of the MPI functions discussed in the previous post. I will start by discussing the essential parts of every MPI program and then go over more specific examples on how to deal with synchronous and asynchronous communcation.
I will illustrate this using Visual Studio and MPICH2. Please bear in mind that the codes are universal, and if you are a UNIX user, then you will have no problem compiling the codes presented hereafter. I chose Visual Studio because I am currently satisfied with the approach that Microsoft is using regarding programming, open source codes, and the .Net technology. That's my biased opinion, but whether you like it or not, Visual Studio is the most versatile and easy to use IDE and compiler on the planet! and the best of all, you can get it for free!
First, lets get visual studio ready. If you have not done so, please refer to "
MPICH2 and Visual Studio" article.
Now start visual studio and create a new C++ EMPTY project (Win32 console application). Call it whatever you want, say MPIWarmup. Then, in the folder browser, right click on "Source files" and create a new C++ source file. Call it "main.cpp". Now we are ready to get started with MPI programming.
First Principles: Your First Parallel Program!
In science, a strong theory is always derived from first principles. These are essentially the conservation laws of mass, momentum, energy etc... In MPI, there are also some first principles to make a code run in parallel.
First of all, before you do anything, you have to include the mpi header file, i.e.
#include <mpi.h>
Every MPI program has to start and end with two very specific functions, respectively. These are:
int MPI_Init(int *argc, char ***argv)
int MPI_Finalize()
all the programming will take place between these two functions. So, here's how it would look like in an actual program:
#include <mpi.h>
#include <stdio.h>
int main(int argc, char* argv[]) {
// initialize the MPI world
MPI_Init(&argc,&argv);
// each processor will print "Bonjour Y'all!"
printf("Bonjour Y'all! \n");
// shutdown the MPI world before exiting
MPI_Finalize();
return 0;
}
To run this program, you need to start a command prompt, and browse to the directory where your code was compiled. Usually, this would be the debug folder of your project directory. Here's a video that summarizes the above.
Here, I ran two instances of the code, that's why you see the message "Bonjour Y'all!" printed twice. This is the simplest MPI program ever, and it does not have any kind of messages sent back and forth of course.
Now let us improve our program a little bit. How about adding the processor "rank" or ID to the printed message. To do this, each processor has to call the MPI rank function. Here's how it is usually done:
#include <mpi.h>
#include <stdio.h>
int processorID;
int numberOfProcessors;
int main (int argc, char* argv[]) {
MPI_Init(&argc, &argv);
// get the size of the cluster and store in numberOfProcessors
MPI_Comm_size(MPI_COMM_WORLD,&numberOfProcessors);
// get the rank or the number of the current process and store it in processorID
MPI_Comm_rank(MPI_COMM_WORLD,&processorID);
printf("I am processor %d - Bonjour Y'all! \n", processorID);
MPI_Finalize();
return 0;
}
This program will output the processor number as well as the Bonjour Y'all message. When debugging parallel codes, including the processor number in your print statements is invaluable because it help you pinpoint where the code is breaking. You will find it very useful to place the above piece of code (without the printf statement of course) in all your parallel programs.
Notice that we have used something called MPI_COMM_WORLD in two of the function calls. This is simply the default communicator that is create when you initialize the MPI world. Communicators are like a web that connects different computers together. Sometimes, you might want to define a new communicator that links only a subset of your parallel computer. I have never used that though.
Also, notice the use of the ampersand (&) in front of the numberOfProcessors and processorID variables. By definition, variables in MPI are passed by address because the data is being copied from one memory address to another. I will not get into the details of this, but remember, you can never send a pointer in MPI.
Let us assume now that you want the MASTER node to print something different than the compute nodes. This can be easily done now that we have the processorID at hand. Of course, the root node has processorID "0" by definition. So, in your code, you could include an if statement that checks if the current processorID is zero or not. However, there's a more elegant way of doing it by using some "define" directives as allowed in the C language. Since we're at it, let us also redefine a couple of global variables:
#include <mpi.h>
#include <stdio.h>
#define MASTER (processorID == 0)
#define NODE (processorID != 0)
#define WORLD MPI_COMM_WORLD
int processorID;
int numberOfProcessors;
int main (int argc, char* argv[]) {
MPI_Init(&argc, &argv);
MPI_Comm_size(WORLD,&numberOfProcessors);
MPI_Comm_rank(WORLD,&processorID);
if (MASTER)
printf("Master node says: Bonjour Y'all! \n");
else
printf("Compute node says: Chillax! \n");
MPI_Finalize();
return 0;
}
I think the above code is clear enough as to what it does.
Peer to Peer Communication
It is time now to start experimenting with send and receive operations. As was mentioned in the previous post, there are two kinds of peer-to-peer communcation, i.e. blocking and immediate. We'll start with the blocking send and receive calls. The anatomy of the send function is
int MPI_Send( void *buf, int count, MPI_Datatype datatype, int dest,
int tag, MPI_Comm comm )
where:
- buf: memory address of the data to be sent
- count: number of elements in send buffer
- datatype: datatype of each send buffer element
- dest: rank of the destination processor
- tag: message tag - useful to identify what is coming from where
- comm: communicator - usually MPI_COMM_WORLD
The receive function call has a similar anatomy as follows:
int MPI_Recv( void *buf, int count, MPI_Datatype datatype, int source,
int tag, MPI_Comm comm, MPI_Status *status )
where:
- buf: memeory address of receive buffer
- status: status object - detects the status of the receive operation
- count: maximum number of elements in receive buffer
- datatype: datatype of each receive buffer element
- source: rank of source processor
- tag: message tag - this should match the tag of the send function
- comm: communicator - usually MPI_COMM_WORLD
Here's an example: assume that the master node has a variable that it wants to send to processor 2 (i.e. rank 1). This could be done by using two if statements as follows:
#include <mpi.h>
#include <stdio.h>
#define MASTER (processorID == 0)
#define NODE (processorID != 0)
#define WORLD MPI_COMM_WORLD
int processorID;
int numberOfProcessors;
int main (int argc, char* argv[]) {
int someVariable = 0;
MPI_Init(&argc, &argv);
MPI_Comm_size(WORLD,&numberOfProcessors);
MPI_Comm_rank(WORLD,&processorID);
// set the value of someVarialbe on the Master node only
if (MASTER) someVariable = 10;
// print the value of someVariable on all processors - this should be zero for all
//nodes except the master
printf("Before Send - Processor %i - someVariable = %i \n",processorID,someVari able);
if (MASTER) {
// send someVariable to processor 1, with the tag being
//the rank of the source processor, i.e. 0
MPI_Send(&someVariable,1,MPI_INT,1,0,WORLD);
}
if (processorID == 1) {
// allocate a status variable
MPI_Status theStatus;
// initiate the receive operation from proccor 0.
MPI_Recv(&someVariable,1,MPI_INT,0,0,WORLD,&theStatus);
}
printf("After Send - Processor %i - someVariable = %i \n",processorID,someVariab le);
MPI_Finalize();
return 0;
}
Voila! To send an array, all you need to do is use the array variable name instead of someVariable. Of course, you have to remove the ampersand if your array was declared as a pointer. If your array is declared as a fixed array, then you can keep the ampersand. I never used fixed array unless it is really necessary for internal code management. A code that does not interact with the user, i.e. a code that is not dynamic by nature is useless. That defeats the whole purpose of programming! So here's an example with an array declared using pointers.
#include <mpi.h>
#include <stdio.h>
#include <stdlib.h>
#define MASTER (processorID == 0)
#define NODE (processorID != 0)
#define WORLD MPI_COMM_WORLD
int processorID;
int numberOfProcessors;
int main (int argc, char* argv[]) {
int arraySize = 0; /* the arraySize variable will be entered at the command line */
MPI_Init(&argc, &argv);
MPI_Comm_size(WORLD,&numberOfProcessors);
MPI_Comm_rank(WORLD,&processorID);
/* only one node (usually the master node) should read from the command line */
if (MASTER) {
printf("Please enter the array size: \n");
fflush(stdout);
scanf("%i",&arraySize);
}
/* after the arraySize is read on the master node, the other nodes need to
have that value locally. at this point, the arraySize = 0 on all nodes
except the master node where it is equal to the value entered at the cmd.
a simple broadcast call will send the arraySize from the root to all other nodes */
MPI_Bcast(&arraySize,1,MPI_INT,0,WORLD);
/* declare a new array using malloc */
float* someArray = (float*) malloc(arraySize*sizeof(float));
/* initialize the newly declared array*/
for (int i = 0; i < arraySize; i++) someArray[i] = 0.0;
/* print the newly declared array */
if(processorID == 1) {
for (int i = 0; i < arraySize; i++)
printf("someArray[%i] = %f \n", i, someArray[i]);
printf("------------------------------------------\n");
}
/* change the values on the master node */
if (MASTER)
for (int i = 0; i < arraySize; i++) someArray[i] = 1.0*(i+1);
if (MASTER) {
/* send someArray to processor 1, with the tag being the
rank of the source processor, i.e. 0 */
MPI_Send(someArray,arraySize,MPI_FLOAT,1,0,WORLD);
}
if (processorID == 1) {
// allocate a status variable
MPI_Status theStatus;
// initiate the receive operation from proccor 0.
MPI_Recv(someArray,arraySize,MPI_FLOAT,0,0,WORLD,&theStatus);
}
/* print the values to make sure the array was correctly received */
if(processorID == 1) for (int i = 0; i < arraySize; i++)
printf("someArray[%i] = %f \n", i, someArray[i]);
MPI_Finalize();
return 0;
}
Note that I have used a broadcast call after the root node reads the array size from the command line. I will explain collective communication very shortly.
So far, we've sent data from the root node to the first node. Of course, this can be done between any two processors. One processor may also send different arrays to different processors.
One subtle scenario occurs when all processors are sending and receiving data from each. This may lead to a deadlock if not properly handled using blocking communication. The safest bet in this case is to use asynchronous or immediate communication. I use block based communication when there is a single processor sending different data sets to all the other processors. For example, in CFD, a typical scenario is when the problem is read into the master node and partitioning is subsequently applied, on the master node. Then, the master has to send the partition information and data structures to its processor. This should be done using blocking send and receive. Now, when the processors start doing the computation, data has to be communicated at the partition interfaces. When the partition topology is simple (unidirectional for example) then blocking communication may be used. However, when the topology is complicated (see Fig. 1), then the easiest and safest way to pass on the data at the interface is by using immediate sends and receives.
Cite as:
Saad, T. "Parallel Computing with MPI - Part IX: MPI Warmup".
Weblog entry from
Please Make A Note.
http://pleasemakeanote.blogspot.com/2008/07/parallel-computing-with-mpi-part-ix-mpi.html
(Fig. 1)
(Fig. 1)
(Fig. 2)
(Fig. 3)
(Fig. 4)
(Eq. 1)
(Fig. 1)
(Eq. 2)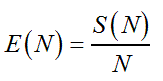
(Eq. 3)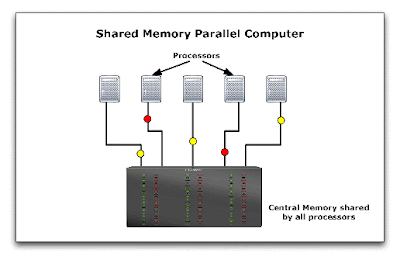
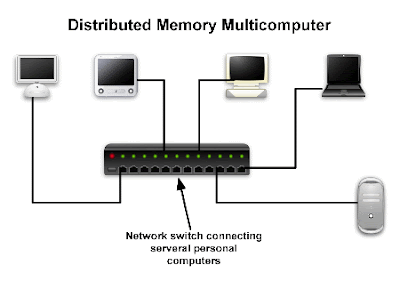
(Eq. 1)
(Eq. 2)
(Eq. 3)
(Eq. 4)
(Eq. 5)
(Eq. 6)
(Eq. 7)
(Eq. 8)
(Eq. 9)
(Eq. 10)
(Eq. 11)
(Eq. 12)
(Eq. 13)
(Eq. 14)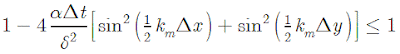
(Eq. 15)
(Eq. 16)
(Eq. 17)
(Eq. 18)
(Eq. 19)
(Eq. 20)
(Eq. 21)
(Eq. 22)
