Please Make A Note: Fluid Mechanics

Showing posts with label Fluid Mechanics. Show all posts

Saturday, July 10, 2010

How Euler Derived the Momentum Equations

In this post, I will present Euler's derivation of the momentum balance equations for a fluid flow. Please note that I will use modern notation with a few modifications to the original derivation to clarify certain issues. Nonetheless, the core of Euler's derivation is maintained.

Considering two dimensional flows with axial and transverse velocities denoted by u(x,y,t) and v(x,y,t), respectively, Euler first forms the total differentials of these fields

$\bg_white \120dpi \begin{cases} {\rm d}u = \dfrac{\partial u}{\partial x}{\rm d}x + \dfrac{\partial u}{\partial y}{\rm d}y + \dfrac{\partial u}{\partial t}{\rm d}t \\[10pt] {\rm d}v = \dfrac{\partial v}{\partial x}{\rm d}x + \dfrac{\partial v}{\partial y}{\rm d}y + \dfrac{\partial v}{\partial t}{\rm d}t \end{cases}$

Next, dividing both equations by dt, we obtain

$\bg_white \120dpi \begin{cases} \dfrac{{\rm d}u}{{\rm d}t} = \dfrac{\partial u}{\partial x}\dfrac{{\rm d}x}{{\rm d}t} + \dfrac{\partial u}{\partial y}\dfrac{{\rm d}y}{{\rm d}t}+ \dfrac{\partial u}{\partial t}\\[10pt] \dfrac{{\rm d}v}{{\rm d}t} = \dfrac{\partial v}{\partial x}\dfrac{{\rm d}x}{{\rm d}t} + \dfrac{\partial v}{\partial y}\dfrac{{\rm d}y}{{\rm d}t} + \dfrac{\partial v}{\partial t} \end{cases}$

but

$\bg_white \120dpi \dfrac{{\rm d}x}{{\rm d}t}=u;\quad {\rm and}\quad \dfrac{{\rm d}y}{{\rm d}t}=v$

then, upon substitution, we recover

$\bg_white \120dpi \begin{cases} \dfrac{{\rm d}u}{{\rm d}t} = u \dfrac{\partial u}{\partial x} + v \dfrac{\partial u}{\partial y}+ \dfrac{\partial u}{\partial t}\\[10pt] \dfrac{{\rm d}v}{{\rm d}t} = u \dfrac{\partial v}{\partial x} + v \dfrac{\partial v}{\partial y} + \dfrac{\partial v}{\partial t} \end{cases}$

One can infer that Euler is heading towards Newton's law. The previous expressions represent the acceleration of a fluid element. As to the forces, Euler identifies pressure, friction, and gravity. For the time being, he abandons friction and focuses on pressure and gravity.

For gravity, the force is in the transverse direction and is given by

$\bg_white \120dpi \quad F_{\rm g,}_x=0; \quad F_{\rm g,}_y = - \mathcal{M} g$

where

$\bg_white \120dpi \mathcal{M}=\rho \mathcal{V} = \rho \, {\rm d}x \, {\rm d}y$

is the mass of the fluid element.

For the pressure, he considers a rectangular fluid element as shown below.

Euler then assumes that the pressure at point L is p and deduces the values at the corners of the control volume. The net force acting on each side is calculated by taking the average pressure at the vertices defining that side and multiplying it by the area. This is shown in the figure below

Then, the net forces in the axial and transverse directions are given by

$\bg_white \120dpi F_x = F_{\rm LN}-F_{\rm MO} = - \dfrac{\partial p}{\partial x}{\rm d}y{\rm d}x$

and

$\bg_white \120dpi F_y = F_{\rm LM}-F_{\rm NO} = - \dfrac{\partial p}{\partial y}{\rm d}x{\rm d}y$

Now, by applying Newton's law, we have

$\bg_white \120dpi \sum \mathbf{F} = \mathcal{M}\frac{{\rm d}\mathbf{u}}{{\rm d}t}$

or, by projecting in both directions, we have

$\bg_white \120dpi F_{\rm g,}_x + F_x = \mathcal{M} \frac{{\rm d}u}{{\rm d}t}$

and

$\bg_white \120dpi F_{\rm g,}_y + F_y = \mathcal{M} \frac{{\rm d}v}{{\rm d}t}$

Upon expansion, we get

$\bg_white \120dpi - \frac{\partial p}{\partial x}{\rm d}x \, {\rm d}y = \rho\,{\rm d}x \, {\rm d}y \left(u \dfrac{\partial u}{\partial x} + v \dfrac{\partial u}{\partial y}+ \dfrac{\partial u}{\partial t} \right )$

and

$\bg_white \120dpi -\rho g \,{\rm d}x \, {\rm d}y - \frac{\partial p}{\partial y}{\rm d}x \, {\rm d}y = \rho\,{\rm d}x \, {\rm d}y \left(u \dfrac{\partial v}{\partial x} + v \dfrac{\partial v}{\partial y} + \dfrac{\partial v}{\partial t} \right )$

Finally, we get the Euler equations

$\bg_white \120dpi \dfrac{\partial u}{\partial t}+ u \dfrac{\partial u}{\partial x} + v \dfrac{\partial u}{\partial y} = - \frac{1}{\rho}\frac{\partial p}{\partial x}$

and

$\bg_white \120dpi \dfrac{\partial v}{\partial t}+u \dfrac{\partial v}{\partial x} + v \dfrac{\partial v}{\partial y} = -\frac{1}{\rho} \frac{\partial p}{\partial y}- g$

Voila!

[Previous: Continuity Eq. in Spherical Coordinates]

[Table of Contents]

[Next: Momentum Eqs. in Cartesian Coordinates]

Cite as:
Saad, T. "How Euler Derived the Momentum Equations". Weblog entry from Please Make A Note. http://pleasemakeanote.blogspot.com/2010/07/how-euler-derived-momentum-equations.html

Sunday, July 4, 2010

9. Derivation of the Continuity Equation in Spherical Coordinates

We start by selecting a spherical control volume dV. As shown in the figure below, this is given by

$\bg_white \120dpi {\rm d}\mathcal{V}=r^2 \sin \theta \,{\rm d}r \,{\rm d}\theta \,{\rm d}\phi$

where r, θ, and φ stand for the radius, polar, and azimuthal angles, respectively. The azimuthal angle is also referred to as the zenith or colatitude angle.

The differential mass is

$\bg_white \120dpi \text{d}\mathcal{M}=r^2 \sin \theta {\rm d}r {\rm d}\theta {\rm d}\phi$

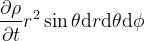
We will represent the velocity field via

$\bg_white \120dpi \mathbf{u}=u \, \mathbf{e}_r + v \, \mathbf{e}_\theta + w \, \mathbf{e}_\phi$

In an Eulerian reference frame mass conservation is represented by accumulation, net flow, and source terms in a control volume.

Accumulation

The accumulation term is given by the time rate of change of mass. We therefore have

$\bg_white \120dpi \frac{\partial \rho}{\partial t}r^2 \sin \theta {\rm d}r {\rm d}\theta {\rm d}\phi$

The net flow through the control volume can be divided into that corresponding to each direction.

Radial Flow

Starting with the radial direction, we have

$\bg_white \120dpi \dot{m}_{\rm in}=\rho \, u \, A_{\rm in}$

The inflow area A_in is a trapezoid whose area is given by

$\bg_white \120dpi A_{\rm in} = \text{mid segment}\times{\rm height}=\tfrac{1}{2}\left[r \sin \theta {\rm d}\phi + r \sin(\theta + {\rm d}\theta){\rm d}\phi \right ]\times r {\rm d}\theta$

The key term here is the sine term. Note that the mid segment is the average of the bases (parallel sides). Upon expansion of A_in, and in the limit of vanishing dθ, we have

$\bg_white \120dpi \sin(\theta + {\rm d}\theta)=\sin\theta \cos{\rm d}\theta + \cos\theta \sin {\rm d}\theta \approx \sin \theta + \cos \theta {\rm d}\theta$

substitution into A_inyields

$\bg_white \120dpi A_{\rm in} = r^2 \sin \theta {\rm d}\theta {\rm d}\phi + \tfrac{1}{2}r^2 \cos \theta {\rm d}\theta^2{\rm d}\phi \approx r^2 \sin \theta {\rm d}\theta {\rm d}\phi$

where high order terms have been dropped.

The outflow in the radial direction is

$\bg_white \120dpi \dot m_{\rm out}=\left(\rho u +\frac{\partial \rho u}{\partial r}{\rm d}r \right )A_{\rm out}$

but

$\bg_white \120dpi A_{\rm out} = \text{mid segment}\times {\rm height}$

where

$\bg_white \120dpi \text{mid segment} = \tfrac{1}{2}\left[(r + {\rm d}r)\sin\theta{\rm d}\phi + (r + {\rm d}r)\sin(\theta + {\rm d}\theta){\rm d}\phi \right ]$

and

$\bg_white \120dpi \text{height} = (r + {\rm d}r){\rm d}\theta$

By only keeping the lowest (second & third) order terms in the resulting expression, we have

$\bg_white \120dpi A_{\rm out}=r^2 \sin \theta {\rm d}\theta {\rm d}\phi + 2 r \sin \theta \, {\rm d}r \, {\rm d}\theta \,{\rm d}\phi$

Note, that in the expression for Aout, we kept both second order and third order terms. The reason for this is that this term will be multiplied by "dr" and therefore, the overall order will be three. In principle, one must carry all those terms until the final substitution is made, and only then one can compare terms and keep those with the lowest order.

At the outset, the net flow in the radial direction is given by

$\bg_white \120dpi \dot{m}_{\rm out}-\dot{m}_{\rm in}=2 \rho \,u \,r \sin \theta \, {\rm d}r \,{\rm d}\theta \,{\rm d}\phi+ \frac{\partial \rho \, u}{\partial r}r^2 \sin \theta \, {\rm d}r \,{\rm d}\theta \,{\rm d}\phi$

Polar Flow (θ)

The inflow in the polar direction is

$\bg_white \120dpi \dot{m}_{\rm in}= \rho \, v \, A_{\rm in}$

where

$\bg_white \120dpi A_{\rm in} = r \sin \theta \,{\rm d}r \,{\rm d}\phi$

The outflow in the θ direction is

$\bg_white \120dpi \dot{m}_{\rm out}=\left(\rho\, v + \frac{\partial \rho\,v}{\partial \theta}{\rm d}\theta \right )A_{\rm out}$

where

$\bg_white \120dpi A_{\rm out}=\tfrac{1}{2}\left[r \sin (\theta + {\rm d}\theta){\rm d}\phi + (r+{\rm d}r)\sin(\theta + {\rm d}\theta){\rm d}\phi \right ]{\rm d}r$

Upon expansion, and keeping both second and third order terms, we get

$\bg_white \120dpi A_{\rm out}\approx r \cos \theta \, {\rm d}r \,{\rm d}\theta \,{\rm d}\phi + r\sin\theta \, {\rm d}r \, {\rm d}\phi$

Finally, the net flow in the polar direction is

$\bg_white \120dpi \dot{m}_{\rm out} - \dot{m}_{\rm in}=\rho \,v\, r \cos\theta \,{\rm d}r \,{\rm d}\theta \,{\rm d}\phi+ \frac{\partial \rho v}{\partial \theta}r \sin \theta \,{\rm d}r \,{\rm d}\theta \,{\rm d}\phi$

Azimuthal Flow (φ)

The inflow in the azimuthal direction is given by

$\bg_white \120dpi \dot{m}_{\rm in}=\rho\,w A_{\rm in}$

with

$\bg_white \120dpi A_{\rm in} = r \,{\rm d}r \,{\rm d}\theta$

while the outflow is

$\bg_white \120dpi \dot{m}_{\rm out} = \left(\rho w + \frac{\partial \rho w}{\partial \phi}{\rm d}\phi \right )A_{\rm out}$

and

$\bg_white \120dpi A_{\rm out}= r \, {\rm d}r \, {\rm d}\theta$

At the outset, the net flow in the polar direction is

$\bg_white \120dpi \dot{m}_{\rm out}-\dot{m}_{\rm in} = \frac{\partial \rho w}{\partial \phi}r \, {\rm d}r \,{\rm d}\theta\,{\rm d}\phi$

Continuity Equation

Now, by collecting all mass fluxes we have

$\bg_white \120dpi \frac{\partial \rho}{\partial t}{\rm d}\mathcal{V}+2 \rho \,u \,\frac{{\rm d}\mathcal{V}}{r}+ \frac{\partial \rho \, u}{\partial r}{\rm d}\mathcal{V}+\rho v \cos \theta \frac{{\rm d}\mathcal{V}}{r \sin \theta} + \frac{\partial \rho v}{\partial \theta}\frac{{\rm d}\mathcal{V}}{r} + \frac{\partial \rho w}{\partial \phi}\frac{{\rm d}\mathcal{V}}{r \sin \theta}=0$

which, upon dividing by dV and combining terms, reduces to

$\bg_white \120dpi \frac{\partial \rho}{\partial t}+\frac{1}{r^2}\frac{\partial \rho \,r^2 u}{\partial r}+\frac{1}{r \sin \theta}\frac{\partial \rho v \sin\theta}{\partial \theta} +\frac{1}{r \sin \theta} \frac{\partial \rho w}{\partial \phi}=0$

which is the continuity equation in spherical coordinates.

Voila!

[Previous: Continuity Eq. in Cylindrical Coordinates]

[Table of Contents]

[Next: How Euler Derived the Momentum Equations]

Cite as:
Saad, T. "9. Derivation of the Continuity Equation in Spherical Coordinates". Weblog entry from Please Make A Note. http://pleasemakeanote.blogspot.com/2010/02/9-derivation-of-continuity-equation-in.html

Saturday, July 3, 2010

Integrating Exact Differentials

Often times I am faced with the integration of a system of differential equations of the form

$\bg_white \120dpi \bg_white \120dpi \begin{cases} \dfrac{\partial p}{\partial x} = S(x,y) \\[12pt] \dfrac{\partial p}{\partial y} = T(x,y) \end{cases}$

This system describes the behaviour of the primitive function "p". In fact, these equations stem from the total differential of p

$\bg_white \120dpi {\rm d}p = \frac{\partial p}{\partial x} {\rm d}x +\frac{\partial p}{\partial y} {\rm d}y$

Two cases arise in this situation. If "dp" is an exact differential, then the system is integrable independent of the path of integration. A differential equation "dp" is said to be an exact differential if the primitive function "p" exists. A necessary and sufficient condition for "dp" to be an exact differential if "p" is continuous and twice differentiable. In other words, when the mixed derivatives of "p" exist and are equal. For example, given

$\bg_white \120dpi {\rm d}p = \frac{\partial p}{\partial x} {\rm d}x + \frac{\partial p}{\partial y} {\rm d}y + \frac{\partial p}{\partial z} {\rm d}z$

then, "dp" is an exact differential if, and only if,

$\bg_white \120dpi \begin{cases} \dfrac{\partial^2 p}{\partial x \partial y} =\dfrac{\partial^2 p}{\partial y \partial x} \\[12pt] \dfrac{\partial^2 p}{\partial x \partial z} =\dfrac{\partial^2 p}{\partial z \partial x} \\[12pt] \dfrac{\partial^2 p}{\partial y \partial z} =\dfrac{\partial^2 p}{\partial z \partial y} \end{cases}$

If the total differential is not exact, then the integration can only be carried out along a specified path of the domain.

Integration of an Exact Differential

The typical approach to integrating the system of differential equations is to first integrate in one coordinate direction, add a function of the remaining coordinates, substitute into the remaining equations and so on.

However, there is another technique that only requires the following three steps:

Integrate each equation with respect to its coordinate without adding any integration constants
Add the results
Subtract the common part

Here's an example. Consider

$\bg_white \120dpi \bg_white \120dpi \bg_white \120dpi \begin{cases} \dfrac{\partial p}{\partial x} = 2xy + y^3 \cos x + \sin(x) \\[12pt] \dfrac{\partial p}{\partial y} = x^2 + 3y^2 \sin x \end{cases}$

Integrating in each direction, we get

$\bg_white \120dpi \bg_white \120dpi \bg_white \120dpi \begin{cases} p_1=\displaystyle{\int \dfrac{\partial p}{\partial x}{\rm d}x} = x^2y + y^3 \sin x - \cos x + c_1 \\[12pt] p_2=\displaystyle{\int \dfrac{\partial p}{\partial y}{\rm d}y} = x^2y + y^3 \sin x + c_2\end{cases}$

Then, the primitive function is

$\bg_white \120dpi p=p_1 + p_2 - p_{\rm commom}$

$\bg_white \120dpi \bg_white \120dpi p=x^2y + y^3 \sin x - \cos x + c$

While this methods works, I have not seen any proof of why it does. Therefore, in this post, I will provide an independent proof. To simplify the process, I will only present this in two dimensions. I will also provide two methods for proving this. The words integral and primitive will be used interchangeably. Furthermore, I will refer to the individual differentials of a function as its constitutive differentials. For example,

$\bg_white \120dpi \inline \dfrac{\partial p}{\partial x}; \quad \dfrac{\partial p}{\partial y}$

are called the constitutive differentials of "p".

Method 1:

A differential system of equations can be written in general as

$\bg_white \120dpi \bg_white \120dpi \begin{cases} \dfrac{\partial p}{\partial x} = f(x) + g(y) + h(x,y) \\[12pt] \dfrac{\partial p}{\partial y} = s(x) + l(y) + q(x,y)\end{cases}$

and let "p1" and "p2" denote the integrals of the above equations without the addition of an integration constant. Thus

$\bg_white \120dpi \begin{cases} p_1=\displaystyle\int \dfrac{\partial p}{\partial x} {\rm d}x = \int f(x){\rm d}x + \int g(y){\rm d}x + \int h(x,y) {\rm d}x \\[12pt] p_2=\displaystyle\int \dfrac{\partial p}{\partial y} {\rm d}y = \int s(x){\rm d}y + \int l(y){\rm d}y + \int q(x,y) {\rm d}y\end{cases}$

Now let us first integrate in the "x" direction

$\bg_white \120dpi \bg_white \120dpi p(x,y)=\int\dfrac{\partial p}{\partial x}{\rm d}x = \int f(x){\rm d}x + \int g(y) {\rm d}x + \int h(x,y) {\rm d}x + N(y)$

$\bg_white \120dpi \bg_white \120dpi \bg_white \120dpi p(x,y) = p_1 + N(y)$

Note the addition of the integration constant "N(y)". Substituting into the second differential, we get

$\bg_white \120dpi \bg_white \120dpi \dfrac{\partial p}{\partial y} = s(x) + l(y) + q(x,y) =\dfrac{\partial }{\partial y}\left[ \int g(y) {\rm d}x \right ]+ \dfrac{\partial }{\partial y}\left[\int h(x,y) {\rm d}x \right ] +\dfrac{{\rm d}N}{{\rm d}y}$

$\bg_white \120dpi \bg_white \120dpi \dfrac{{\rm d}N}{{\rm d}y} = s(x) + l(y) + q(x,y)-\dfrac{\partial }{\partial y}\left[ \int g(y) {\rm d}x \right ] - \dfrac{\partial }{\partial y}\left[\int h(x,y) {\rm d}x \right ]$

(Note that it is assumed here that dN/dy is a function of y ONLY, so that the right hand side of the above equation will evaluate of a function of y and only y). Integrating with respect to "y", we recover

$\bg_white \120dpi \bg_white \120dpi N(y) = \int s(x){\rm d}y + \int l(y){\rm d}y + \int q(x,y){\rm d}y - \int g(y) {\rm d}x - \int h(x,y){\rm d}x + c$

$\bg_white \120dpi \bg_white \120dpi \bg_white \120dpi N(y) = p_2 - \int g(y) {\rm d}x - \int h(x,y){\rm d}x + c$

substituting "N(y)" into the equation for "p(x,y)", we have

$\bg_white \120dpi p(x,y) = p_1 + p_2 \underbrace{-\int g(y) {\rm d}x - \int h(x,y){\rm d}x}_{-M(x,y)} + c$

So far, we have shown that the primitive function is the sum of the integrals in each direction (i.e. p1 and p2) minus some term denoted by M(x,y). It remains to show that M(x,y) represents a part that is common to both "p1" and "p2". To arrive at this, we invoke the fact that the this system's total differential is exat, i.e.

$\bg_white \120dpi \dfrac{\partial^2 p}{\partial x \partial y} =\dfrac{\partial^2 p}{\partial y \partial x}$

$\bg_white \120dpi \dfrac{\partial g}{\partial y} + \dfrac{\partial h}{\partial y} = \dfrac{\partial s}{\partial x} + \dfrac{\partial q}{\partial x}$

collecting terms, we get

$\bg_white \120dpi \dfrac{\partial (g + h)}{\partial y} = \dfrac{\partial (s + q)}{\partial x}$

This is true if

$\bg_white \120dpi \begin{cases} g(y)+h(x,y) = \dfrac{\partial T(x,y)}{\partial x}\\[12pt] s(x)+q(x,y) = \dfrac{\partial T(x,y)}{\partial y} \end{cases}$

with T(x,y) being continuous and twice differentiable. Given this, we rewrite M(x,y) as

$\bg_white \120dpi M(x,y) = \int \left[g(y)+h(x,y) \right ]{\rm d}x=\int \dfrac{\partial T}{\partial x}{\rm d}x=T(x,y)$

Finally, we now rewrite "p1" and "p2" using T(x,y)

$\bg_white \120dpi \begin{cases} \displaystyle p_1= \int f(x){\rm d}x + T(x,y) \\[12pt] \displaystyle p_2= \int l(y){\rm d}y + T(x,y) \end{cases}$

It is therefore clear that M(x,y) is actually a common term for "p1" and "p2" and the primitive is given by

$\bg_white \120dpi p(x,y) = p_1 + p_2 - T(x,y) + c$

Q.E.D.

Note: One can now verify that the integration constant N(y) is a function of y, and only y. Reconsider the equation for dN/dy

writing in terms of T(x,y), we have

$\bg_white \120dpi \dfrac{{\rm d}N}{{\rm d}y} = l(y) + \dfrac{\partial T}{\partial y} -\dfrac{\partial }{\partial y}\underbrace{\left\{ \int \left[ g(y) + h(x,y)\right ] {\rm d}x \right\}}_{T(x,y)}$

$\bg_white \120dpi \dfrac{{\rm d}N}{{\rm d}y} = l(y) + \dfrac{\partial T}{\partial y} -\dfrac{\partial T}{\partial y}=l(y)$

Method 2:

Consider a real continuous and twice differentiable function "p(x,y)". In general, this function can be written as

$\bg_white \120dpi \bg_white \120dpi p(x,y)=f(x) + g(y) + q(x,y) + c$

where "c" is a constant and the component functions are also real, continuous, and twice differentiable. Now form the total differential of "p"

$\bg_white \120dpi {\rm d}p = \frac{\partial p}{\partial x} {\rm d}x +\frac{\partial p}{\partial y} {\rm d}y$

where

$\bg_white \120dpi \begin{cases} \dfrac{\partial p}{\partial x} = \dfrac{{\rm d}f}{{\rm d}x} + \dfrac{\partial q}{\partial x} \\[12pt] \dfrac{\partial p}{\partial y} = \dfrac{{\rm d}g}{{\rm d}y} + \dfrac{\partial q}{\partial y} \end{cases}$

The key component of this derivation are the derivatives of "q" in both differentials. We now define the integrals of the above system without adding an integration constant. We get

$\bg_white \120dpi \begin{cases} p_1=\displaystyle\int \dfrac{\partial p}{\partial x} {\rm d}x = f(x) + q(x,y) + c_1\\[12pt] p_2=\displaystyle\int \dfrac{\partial p}{\partial y} {\rm d}y = g(y){\rm d}y + q(x,y) + c_2 \end{cases}$

but we know that

$\bg_white \120dpi \bg_white \120dpi p(x,y)=f(x) + g(y) + q(x,y) + c$

When written in terms of "p1" and "p2", one recovers

$\bg_white \120dpi p(x,y)= p_1 + p_2 - q(x,y)$

where q(x,y) is the common part.

Q.E.D.

This shows that the primitive of an exact differential is equal to the sum of primitives of its constitutive functions minus the common part. Integration of the constitutive differentials is carried out without adding integration constants.

Summary:

While I have shown that the method of separate integrations works, one must remember that this technique is applicable ONLY to exact differentials. Therefore, the mixed derivatives test must be first applied before carrying out this type of integration. In my next post, I will discuss how to handle inexact differentials.

Cite as:
Saad, T. "Integrating Exact Differentials". Weblog entry from Please Make A Note. http://pleasemakeanote.blogspot.com/2010/07/integrating-totalexact-differentials.html

Pages

Saturday, July 10, 2010

How Euler Derived the Momentum Equations

Sunday, July 4, 2010

9. Derivation of the Continuity Equation in Spherical Coordinates

Accumulation

Radial Flow

Polar Flow (θ)

Azimuthal Flow (φ)

Continuity Equation

Saturday, July 3, 2010

Integrating Exact Differentials

Integration of an Exact Differential

Method 1:

A differential system of equations can be written in general as

Method 2: