[Previous Article: The Material Derivative in Vector Form]
For completion purposes, I feel obliged to discuss the Reynolds transport theorem. Although I would like to derive the fluid flow equations from scratch, the Reynolds transport theorem provides an avenue for a simple way to derive them. Henceforth, I decided to use the many ways of deriving the conservation equations, whether in integral or differential form.
I will base the current derivation on the text by James A. Fay Introduction to Fluid Mechanics. I believe it is an excellent text on fluid mechanics that focuses on the essential physics of fluid flows.
We first have to distinguish between a material volume and a control volume. A material volume is a volume of fluid that contains the same fluid as it moves and deforms in time.
A control volume is a fixed volume in space where the fluid passes through.
This is tightly linked to the previous discussions on the material derivative and its connection with the Lagrangian and Eulerian views. A material volume is part of a Lagrangian description whereas a control volume is part of the Eulerian description.
Now let us consider and "extensive" property B whose "intensive" property is b. For example, mass is an extensive property, whereas the density is the corresponding intensive property. An extensive property describes a specific part of the fluid (e.g. the mass is different for different volumes of the same fluid) while the intensive property is intrinsic (e.g. the density is the same for different volumes of the same fluid). In simple terms, an intensive property is the extensive property per unit mass.
The Reynolds transport theorem can be thought of as the integral form of the material derivative. It mainly relates the rate of change of an extensive property of a given material volume to the rate of change of the corresponding intensive property.
The total amount of property B in a given material volume is therefore
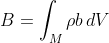
(Eq. 1)
As the material volume moves around, the quantity B inside M changes due to external forces or internal reactions for example. Therefore, it is convenient to compute the time rate of change of B
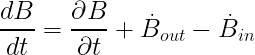
(Eq. 2)
Eq. 2 means that the rate of change of the quantity B in the material volume is equal to the rate of change of B within the fixed control volume plus the net flowrate of the quanity B through the control surface. The RHS of Eq. 2 can be expressed as follows
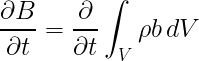
(Eq. 3)
and
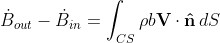
(Eq. 4)
Eq. 4 measures the flux of the quantity B through the control surface. Then, combining the above equations, we get the Reynolds transport theorem
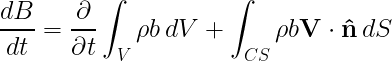
(Eq. 5)
Voila!
For completion purposes, I feel obliged to discuss the Reynolds transport theorem. Although I would like to derive the fluid flow equations from scratch, the Reynolds transport theorem provides an avenue for a simple way to derive them. Henceforth, I decided to use the many ways of deriving the conservation equations, whether in integral or differential form.
I will base the current derivation on the text by James A. Fay Introduction to Fluid Mechanics. I believe it is an excellent text on fluid mechanics that focuses on the essential physics of fluid flows.
We first have to distinguish between a material volume and a control volume. A material volume is a volume of fluid that contains the same fluid as it moves and deforms in time.
A control volume is a fixed volume in space where the fluid passes through.
This is tightly linked to the previous discussions on the material derivative and its connection with the Lagrangian and Eulerian views. A material volume is part of a Lagrangian description whereas a control volume is part of the Eulerian description.
Now let us consider and "extensive" property B whose "intensive" property is b. For example, mass is an extensive property, whereas the density is the corresponding intensive property. An extensive property describes a specific part of the fluid (e.g. the mass is different for different volumes of the same fluid) while the intensive property is intrinsic (e.g. the density is the same for different volumes of the same fluid). In simple terms, an intensive property is the extensive property per unit mass.
The Reynolds transport theorem can be thought of as the integral form of the material derivative. It mainly relates the rate of change of an extensive property of a given material volume to the rate of change of the corresponding intensive property.
(Eq. 1)
As the material volume moves around, the quantity B inside M changes due to external forces or internal reactions for example. Therefore, it is convenient to compute the time rate of change of B
(Eq. 2)
Eq. 2 means that the rate of change of the quantity B in the material volume is equal to the rate of change of B within the fixed control volume plus the net flowrate of the quanity B through the control surface. The RHS of Eq. 2 can be expressed as follows
(Eq. 3)
(Eq. 4)
(Eq. 5)
Voila!
There is an alternative way of deriving the Reynolds transport theorem, however, it makes use of the continuity equation which we have not derived yet. So this will be postponed to a later post.
[Next Article: How Euler Derived the Continuity Equation]
[Next Article: How Euler Derived the Continuity Equation]
Cite as:
Saad, T. "5. The Reynolds Transport Theorem".
Weblog entry from
Please Make A Note.
http://pleasemakeanote.blogspot.com/2008/09/derivation-of-navier-stokes-equations.html


The method of explaining is very good...This is the most understandable explanation of Reynolds Transport theorem I ever had read..Thanks...
ReplyDeleteThanks a lot!
ReplyDeleteThe \reverse part in latex formulas is making it look ugly. Nice note by the way!
ReplyDeleteThe reverse color for the equations was reminiscent of the old blog with the black background. I just corrected that.
ReplyDelete"In simple terms, an intensive property is the extensive property per unit mass."
ReplyDeleteI think you meant 'per unit volume'
Actually, it is 'per unit mass' in his case
DeleteThank you for the explanation about the RTT. I seen something quite puzzling about all the derivations i have encountered. About equation 2 in the derivation: If the time derivative on the lefthand side is taken to be increasing(B increases with time) then the quantity of B in the volume should be increasing: Hence on the RHS we should have B(in) - B(out)!
ReplyDeleteI was looking for this information, thanks for put in this easy way, I mean in a easy way to understand it jajaja, well until the next time.
ReplyDeletethanq.....
ReplyDelete