Dot and cross products are invariant under coordinate transformation, so they have the same form for all coordinates
and
The remaining operations take specific forms under different coordinates. For Cylindrical coordinates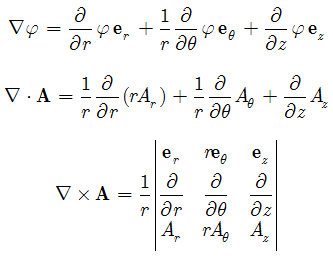
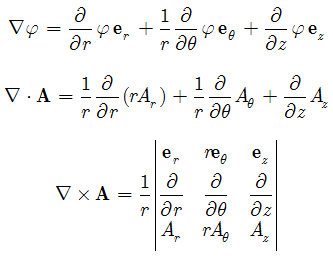
Voila!
P.S. most people refer to the "inverted triangle" operator as the "del" operator; however, this symbol is called "nabla" just like epsilone, eta, gamma etc... and I find no reason for calling it otherwise! Therefore, I usually use terms such as "nabla phi" for the gradient of a scalar, "nabla dot A" and "nabla cross A" for the divergence and curl of a vector field, respectively.
P.S. most people refer to the "inverted triangle" operator as the "del" operator; however, this symbol is called "nabla" just like epsilone, eta, gamma etc... and I find no reason for calling it otherwise! Therefore, I usually use terms such as "nabla phi" for the gradient of a scalar, "nabla dot A" and "nabla cross A" for the divergence and curl of a vector field, respectively.
Cite as:
Saad, T. "Vector (Nabla) Operations in Curvilinear Coordinates".
Weblog entry from
Please Make A Note.
https://pleasemakeanote.blogspot.com/2008/05/nabla-operations-gradient-curl-and-dot.html

Hey, thanks for posting these formulas! These came in handy for my homework.
ReplyDeleteYes, Nabla is the name for that inverse triangle symbol (typographically), but Del is the name for the differential operator denoted using Nabla symbol. So, if you're not referring to the symbol itself, but to the differential operation, Del is the better option.
ReplyDeleteThanks for your comment. I do not agree with you on that point because the "del" terminology is used in the following context: "del dot u" or "del cross u" which is not the actual name of the mathematical operations "divergence of u" and "curl u". Therefore, "del" is used to designate the "nabla" symbol which is called "nabla".
ReplyDeleteyNot,
ReplyDeleteIf you're dealing with dinosaurs, "del" is pretty much hardwired.
Also, I believe the term divergence is limited to 3D, where the operator del exists for all dimensions. Since the cross product only exists in 3D (it has no obvious analog in 4D, for instance), there is no "other operator" which is more general.
I have never seen the operator termed "nabla" outside of LaTeX books. "Del" has a relatively wide use, and you'll get blank stares if you use the term "nabla" to denote the operator.
Interesting blog, by the way. Found it in lookup up what \printglossary had turned into when I was attempting to reprocess an old paper.
Thanks!
Nabla is the name of the ∇ symbol, which is the inverted Greek Delta (Δέλτα).Its Greek name is anadelta (ανάδελτα).ανα=upside down+δέλτα.
ReplyDeleteHi !
ReplyDeleteMay I ask , what program did you use when you created the first big image (when you describing for Cylindrical coordinates)
this is beautiful..
Thanks!
I found it in MathType's Miscellaneous symbols pallet if that helps. In MathType it's refered to as "Gradient (nabla) from Symbol style" "del" isn't mentioned anywhere.
ReplyDeleteNice way to buy a vector with a easy method, you're a genius! thanks for post this useful formula.
ReplyDeleteThanks for sharing. Never calculated it like that. Always used a different way.
ReplyDelete