Download Mathematica notebook [right click / save as]
To generate the 2D phase space, use this simple code
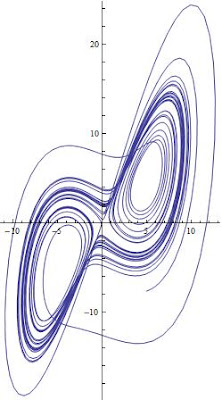
To generate the 3D phase space, use the ParametricPlot3D[] as follows
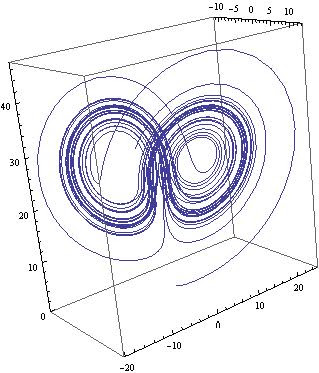 Voila!
Voila!
Download Mathematica notebook [right click / save as]
In a previous article, I discussed how one can use the NDSolve[] utility in Mathematica to obtain a numerical solution for a set of ODEs using the Lorenz equations as a representative example. In this article, I will show how easy it easy to plot the phase space diagram which represents all possible states for a given system. In the case of the Lorenz equations, the phase space is three dimensional because there are three variables: x, y, and z. But of course, one can always study subsets of the 3D phase space, i.e. x vs y for instance. To accomplish this, we make use of the numerical data generated in the previous article, and employ two function in Mathematica; ParametricPlot[] for 2D and ParametricPlot3D[] for 3D spaces.
To generate the 2D phase space, use this simple code
ParametricPlot[Evaluate[{x[t], y[t]} /. s1], {t, 0, Tend}, PlotRange -> All]

To generate the 3D phase space, use the ParametricPlot3D[] as follows
ParametricPlot3D[Evaluate[{x[t], y[t], z[t]} /. s1], {t, 0, Tend},PlotRange -> All]
 Voila!
Voila!Of course, s1 was obtained in Part I of this series and represents the numerical solution for the Lorenz equations.
Download Mathematica notebook [right click / save as]
Thanks!!
ReplyDeleteYou've just saved me hours of research, and this is not the first time you help me.
Federico, from Argentina
Thanks for your feedback!
ReplyDeleteThank ye Very Much Ye unkown friend... this was a great help!
ReplyDeleteSolving Differential Equations with Mathematica is perfect it's something really exciting for me because math is my passion, I remember when math was really complicate for me and now is my life style
ReplyDeleteit was some of the most difficult thing in my cycle in the school and high school!Impressive and attractive posting. I enjoyed it. I think others will like it & find it useful for them. Good luck with your work
ReplyDelete