This article will be a very long one, albeit I hate to write long articles on a blog. So if you would like me to split it, just drop me a comment or an email.
What is Parallel Computing?
For example, a code that computes the sum of the first N integers is very easy to program in parallel. Each processor will be responsible for computing a fraction of the global sum. However, at the end of the execution, all processors have to communicate their local sums to a single processor for example that will add them all up to obtain the global sum.
Types of Parallel Computers
There two types of parallel architectures
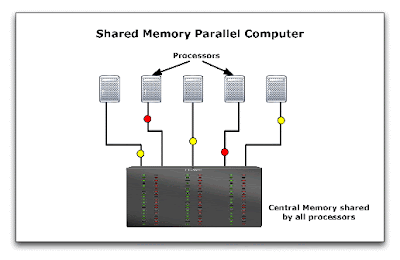
- Shared memory multiprocessor
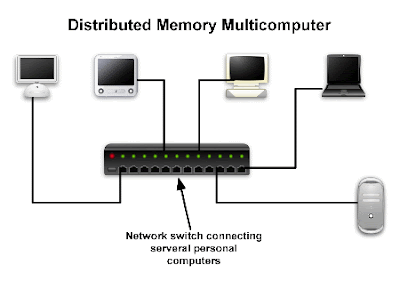
- Distributed memory multicomputer
In a distributed memory configuration, each processor has its own memory addresses and data has to be sent from one processor to another. Computers are usually connected via network switch and data flows over the network from one processor to another. Note, however, that multi-core CPUs as well as multi-socket motherboards CAN use this configuration. In this case, although the memory modules are the same for all processors, each one of them reserves a portion of this memory just as if it existed independently of the others. Also, when multi-core systems are used, data is sent much faster since it does not have to go through a network. The main advantage of this configuration is robustness. For example, new machines can always be added to the parallel computer. Office computers can be used as part of the parallel computer when they are idle, and if the GRAs do not work overnight!
So How Does it Work?
The history of parallel computing extends over a long period of time and may be traced to the early 60's (check this link for a concise historical perspective). However, the most important milestone took place in 1992 when a bunch of scientist (most likely computer guys) were assembled to create a standard for message passing; their job was to formulate a universal framework for exchanging data in a parallel computer. So they retreated for a while and came up with what is called today the Message Passing Interface or MPI. It defines a set of functions and rules on how data is to flow from one processor to another within a parallel computer. Of course, they do not have to do the actual implementation as this is left for third party vendors or the open source community.
So how does parallel computing work? The notion is very simple. A computer code runs on different processors. At one point or another, data has to be exchanged between processors. Therefore, a functional call has to be included at that point to instruct the code to send or receive data. Once the executable reaches that line of code, it allocates some memory on the CPU buffer, copies the data that is to be sent, and sends this data to the receiving computer. On the receiving end, the code is waiting for some data to arrive. Of course, it knows what it will be receiving, therefore it allocates enough space in the CPU buffer and waits for this data. Once the data arrives, it copies it to the designated address in memory. and that's all!
Of course, there are many other ways that this happens, and different implementations do things differently, but the scenario presented above is one viable method. I still have to include some references though.
 (Eq. 1)
(Eq. 1) (Eq. 2)
(Eq. 2) (Eq. 3)
(Eq. 3) (Eq. 4)
(Eq. 4) (Eq. 5)
(Eq. 5) (Eq. 6)
(Eq. 6) (Eq. 7)
(Eq. 7) (Eq. 8)
(Eq. 8) (Eq. 9)
(Eq. 9) (Eq. 10)
(Eq. 10) (Eq. 11)
(Eq. 11) (Eq. 12)
(Eq. 12) (Eq. 13)
(Eq. 13) (Eq. 14)
(Eq. 14)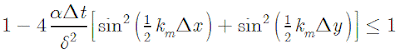 (Eq. 15)
(Eq. 15) (Eq. 16)
(Eq. 16) (Eq. 17)
(Eq. 17) (Eq. 18)
(Eq. 18) (Eq. 19)
(Eq. 19) (Eq. 20)
(Eq. 20) (Eq. 21)
(Eq. 21) (Eq. 22)
(Eq. 22)








